ফার্মার্টের নীতি
1. Three right angled prisms of refractive indices , and are joined together ao that the faces of the middle prism are each in contact with one of the outside prisms. If the ray passes through the composite block undeviated, then
Ai এর মাধ্যমে
১০ লক্ষ+ প্রশ্ন ডাটাবেজ
প্র্যাকটিস এর মাধ্যমে নিজেকে তৈরি করে ফেলো
উত্তর দিবে তোমার বই থেকে ও তোমার মত করে।
সারা দেশের শিক্ষার্থীদের মধ্যে নিজের অবস্থান যাচাই
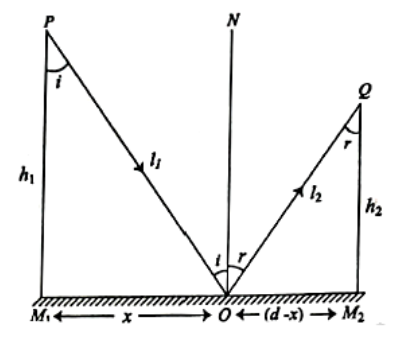চিত্রে আলোকরশ্মি P বিন্দু থেকে POQ পথে Q বিন্দু পর্যন্ত দূরত্ব অতিক্রম করতে প্রয়োজনীয় সময় t হলে,
ফার্মাটের নীতি অনুযায়ী প্রযোজ্য হলো -
A ray of light of wavelength and frequency enters a glass slab of refractive index from air. Then,
কাগজের ভার হিসেবে ব্যবহৃত একটি পুরো কাচ(প্রতিসরণাঙ্ক 1.5 ) খন্ডের উপর থেকে খাড়া নিচের দিকে তাকালে কাগজের উপর একটি দাগ কাচের উপর প্রান্ত থেকে নিচে দেখা যায়। কাচ খন্ডটির পুরত্ব কত ? (কাগজের দাগটি কাচের উপর প্রান্ত থেকে 6cm নিচে)
ফার্মাটের নীতির সাহায্যে ব্যাখ্যা করা যায়-
আলোর সরলরৈখিক গতি
আলোর প্রতিফলন ও প্রতিসরণ
আলোর অপবর্তন ও সমবর্তন
নিচের কোনটি সঠিক?
